Runge-Kutta

This repository offers basic implementations in Python of Runge-Kutta methods (explicit and implicit) for educational purposes. A damped Newton method is also available with efficient Jacobian reuse. A few test cases are given (heat equation, spring-mass system, Curtiss-Hirschfelder).

Dynamic time step adaptation is implemented for explicit embedded methods.

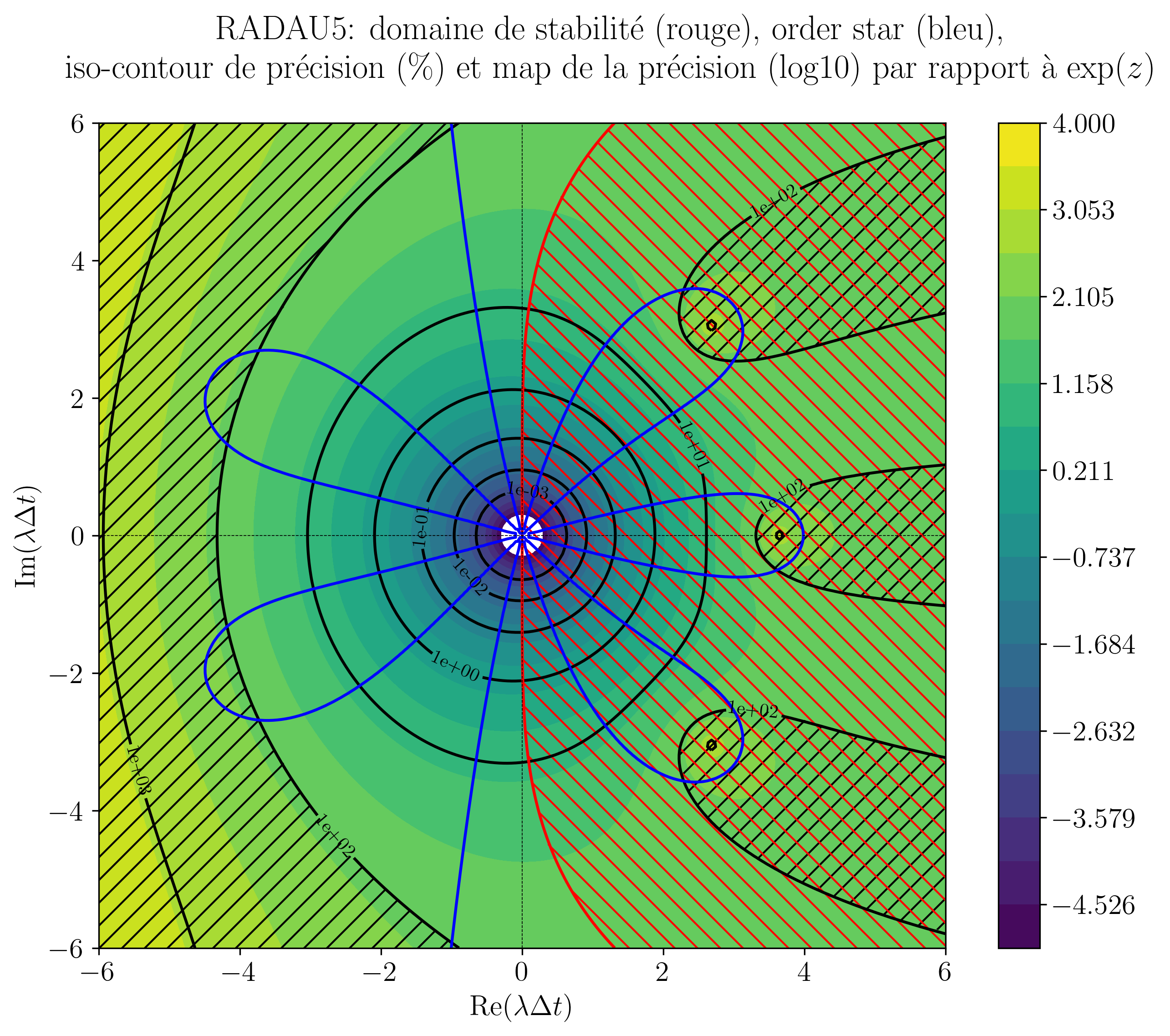
A script is also provided to study the stability domains, order stars and relative precision contours of any Runge-Kutta scheme. Here is the result for the well-known Radau5 scheme:

# TODO: - time step adaptation: - Shampine's trick to L-stabilize the error estimate if necessary - damped newton improvements: - trade between more iterations and more jacobian updates - verify scipy's grouped jacobian determination - stiff PDE test case