通过迭代计算局部最小值点的方法。
机器学习中常见模型,已知损失函数f(w),其中w是权重矩阵,目标是求w,使得f(w)最小。
迭代规则
迭代过程演示:
以
可梯度求解的条件 L-Lipschitz continuous
存在常数
多维举例:
转换成矩阵的写法:
迭代过程:
softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类
交叉熵损失函数经常用于分类问题中,特别是在神经网络做分类问题时,也经常使用交叉熵作为损失函数,此外,由于交叉熵涉及到计算每个类别的概率,所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现
为了进一步区分相同正确率情况下不同模型的好坏。
比如对于三分类问题:
模型A [0.1, 0.1, 0.8], [0.2, 0.7, 0.1], [0.4, 0.6, 0]
模型B [0.1, 0.2, 0.7], [0.2, 0.6, 0.2], [0.1, 0.1, 0.8]
实际结果为 [0, 0, 1], [0, 1, 0], [1, 0, 0]
模型A,B前两个都会判对,但是明显模型A比模型B更优,因为它更接近真实答案。即使是错误的第三个结果。
另一个优点: 求导简单,最优化损失函数。
one-hot
King [1, 0, 0, 0]
Man [0, 1, 0, 0]
Queen [0, 0, 1, 0]
Woman [0, 0, 0, 1]
word vec:
通过计算能体现词之间的关系
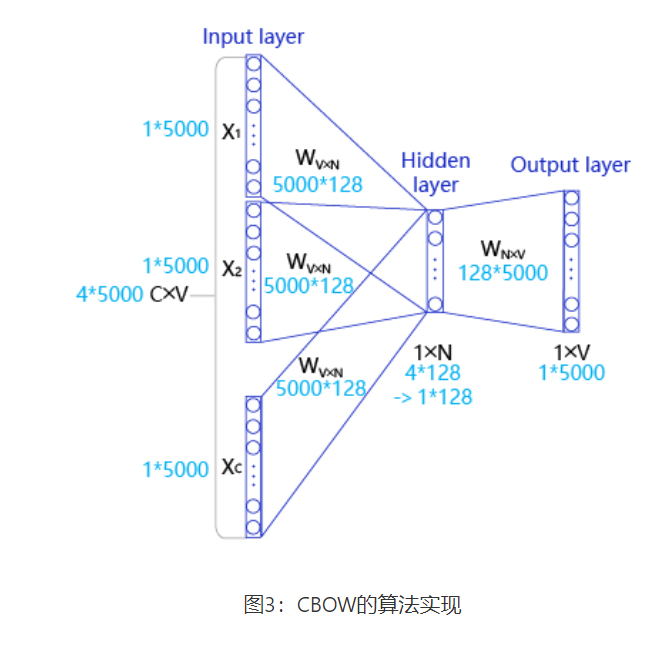
输入层:一个形状为C×V的one-hot张量,其中C代表上线文中词的个数,通常是一个偶数,我们假设为4;V表示词表大小,我们假设为5000,该张量的每一行都是一个上下文词的one-hot向量表示,比如“Pineapples, are, and, yellow”。
隐藏层:一个形状为V×N的参数张量W1,一般称为word-embedding,N表示每个词的词向量长度,我们假设为128。输入张量和word embedding W1进行矩阵乘法,就会得到一个形状为C×N的张量。综合考虑上下文中所有词的信息去推理中心词,因此将上下文中C个词相加得一个1×N的向量,是整个上下文的一个隐含表示。
输出层: 创建另一个形状为N×V的参数张量,将隐藏层得到的1×N的向量乘以该N×V的参数张量,得到了一个形状为1×V的向量。最终,1×V的向量代表了使用上下文去推理中心词,每个候选词的打分,再经过softmax函数的归一化,即得到了对中心词的推理概率:
https://github.com/FraLotito/pytorch-continuous-bag-of-words/blob/master/cbow.py